该笔记是对课上所讲的总结,不全为相似。
相似三角形的判定方法有AA、SAS、SSS、HL,值得注意的是和全等一样,SSA也是无法判定的。
相似三角形除了预备定理外,还有以下重要性质:周长比、对应边上的高长之比、对应元素长度之比皆等于相似比;面积比等于相似比的平方。这些就是最基本的了。
下面来记录一些模型吧。
最基本的就是母子形,射影形是其中一个特例。
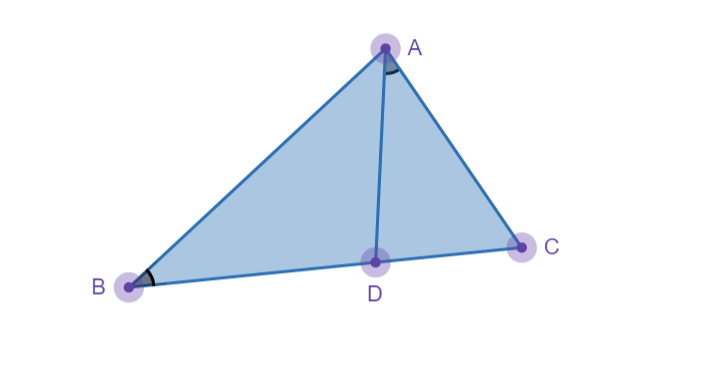
如图,\bigtriangleup ABC中,BC上有一点D,且\angle CAD=\angle B。则\bigtriangleup ABC \sim \triangle CAD,因此AC^2=BC \cdot CD和AB^2=BC \cdot BD \Rightarrow \frac{AB^2}{AC^2}=\frac{BD}{CD}=\frac{S_{\triangle ABD}}{S_{\triangle ADC}}。
还有一个是手拉手。
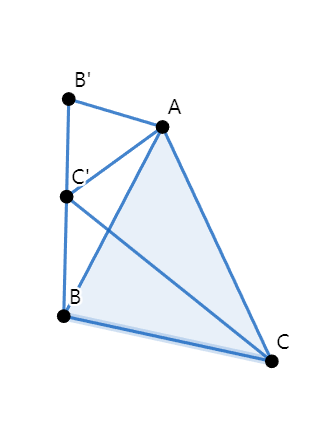
七八年级学习了手拉手证全等,其实其中还有两对相似三角形可以互推。在上图中,\triangle ABC \sim \triangle AB'C' \Leftrightarrow \triangle ABB' \sim \triangle ACC'。特别地,若BC'B'共线,那么ACBC'共圆,用内对角互补可证,反过来也是成立的。
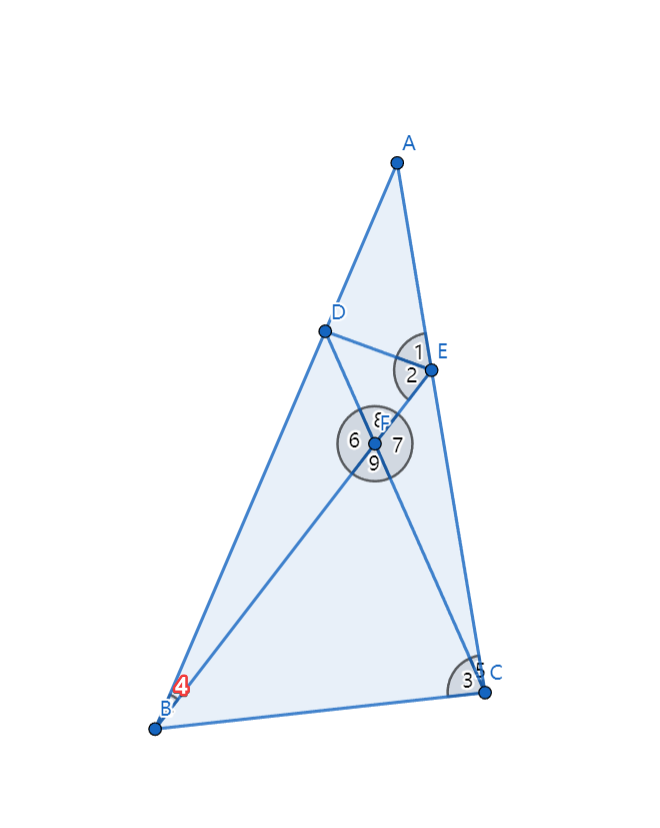
如图所示,\angle 1= \angle ABC是\angle 2= \angle 3的充分必要条件。
\begin{array}{l} \because \angle 1=\angle ABC \\ \angle A= \angle A \\ \therefore \triangle AED \sim \triangle ABC \\ \therefore \frac{AE}{AB} =\frac{AD}{AC} 又\angle A= \angle A \\ \therefore \triangle AEB \sim \triangle ADC \\ \therefore \angle 4=\angle 5 又\angle 6=\angle 7 \\ \therefore \frac{DF}{EF}= \frac{BF}{CF} 又\angle 8=\angle 9\\ \therefore \triangle BFC \sim \triangle DFE \\ \therefore \angle 2=\angle 3 \end{array}反之亦然。latex不好用,就不写了。

你这让我想起我上学时候记录的近代史的笔记了😄
随便记个笔记,玩玩